আপনার গবেষণা পদ্ধতির সাতকাহন: লিনিয়ার রিগ্রেশন
(Linear Regression in Research methodology)
ধরুন, আপনি অনেকগুলো কাঁচামাল জোগাড় করেছেন। এখন সেই কাঁচামাল দিয়ে কী বানাবেন, কীভাবে বানাবেন, সেটাই হলো বিশ্লেষণের কাজ। আর এই বিশ্লেষণের দুনিয়ায় একটা দারুণ 'ম্যাজিক টুল' আছে, যার নাম লিনিয়ার রিগ্রেশন। এর নামটা একটু জটিল শোনালেও, এর কাজটা কিন্তু খুবই সহজ আর কাজের। চলুন, আজ আমরা এই লিনিয়ার রিগ্রেশনের আদ্যোপান্ত জেনে নিই, একদম A2Z!
লিনিয়ার রিগ্রেশন আসলে কী? (What is Linear Regression?)
আচ্ছা, আপনি কি কখনো ভেবে দেখেছেন, একজন শিক্ষার্থী যত বেশি সময় পড়াশোনা করে, তার পরীক্ষার নম্বর তত বাড়ে কেন? অথবা, একটি পণ্যের দাম বাড়লে তার বিক্রি কমে যায় কেন? এই 'কেন' আর 'কীভাবে'র সম্পর্কটা খুঁজে বের করার জন্যই লিনিয়ার রিগ্রেশনকে আমরা ব্যবহার করি।
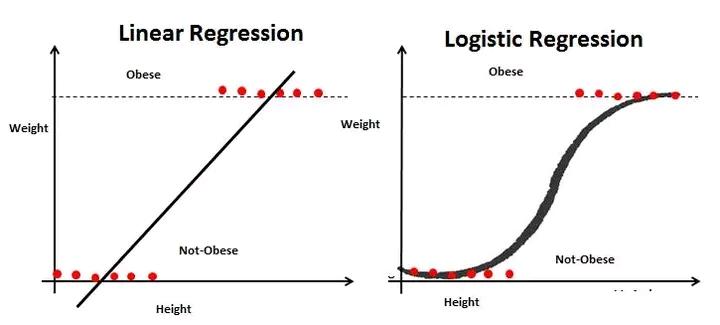
সহজ করে বললে, লিনিয়ার রিগ্রেশন হলো এমন একটি পরিসংখ্যানগত কৌশল, যা দুটি বা তার বেশি বিষয়ের মধ্যে একটা সরলরেখার মতো সম্পর্ক খুঁজে বের করতে সাহায্য করে। এটি অনেকটা একটা অদৃশ্য সুতো খুঁজে বের করার মতো, যা দুটি জিনিসকে একসঙ্গে বেঁধে রাখে। যেমন, পড়াশোনার সময় আর পরীক্ষার নম্বরের মধ্যে একটা সম্পর্ক আছে, তাই না? লিনিয়ার রিগ্রেশন সেই সম্পর্কটাকে একটা সরলরেখা দিয়ে প্রকাশ করে।
এখানে দুটো গুরুত্বপূর্ণ খেলোয়াড় আছে, যাদেরকে আমরা 'চলক' (Variables) বলি:
১। স্বাধীন চলক (Independent Variable): এই হলো সেই 'কারণ' বা 'ইনপুট'। একে আপনি পরিবর্তন করতে পারেন, বা এটি নিজে নিজেই পরিবর্তিত হয় এবং অন্য কোনো কিছুকে প্রভাবিত করে। যেমন, পড়াশোনার সময়, বিজ্ঞাপনের খরচ, বা একটি বাড়ির আকার। ভাবুন তো, পড়াশোনার সময় বাড়লে বা কমলে পরীক্ষার নম্বরের ওপর একটা প্রভাব পড়ে, তাই না?
২। নির্ভরশীল চলক (Dependent Variable): আর এই হলো সেই 'ফলাফল' বা 'আউটপুট', যা স্বাধীন চলকের পরিবর্তনের কারণে প্রভাবিত হয়। যেমন, পরীক্ষার নম্বর, পণ্যের বিক্রি, বা বাড়ির দাম। এই চলকটি স্বাধীন চলকের উপর 'নির্ভর' করে।
লিনিয়ার রিগ্রেশনের মূল লক্ষ্য হলো এই স্বাধীন ও নির্ভরশীল চলকের মধ্যে একটা গাণিতিক সম্পর্ক খুঁজে বের করা, যা দেখতে একটা সরলরেখার মতো। এই রেখার একটা সমীকরণ থাকে: Y=a+bX
এখানে: Y হলো নির্ভরশীল চলক (ফলাফল): অর্থাৎ, আপনি যে জিনিসটা অনুমান করতে চান বা যার পরিবর্তন মাপতে চান।
X হলো স্বাধীন চলক (কারণ): অর্থাৎ, যে জিনিসটা পরিবর্তনের কারণ হিসেবে কাজ করছে।
a হলো ইন্টারসেপ্ট (Intercept): এটি অনেকটা গ্রাফের Y-অক্ষকে রেখাটি যেখানে ছেদ করে সেই বিন্দু। সহজ ভাষায়, যখন স্বাধীন চলক (X) এর মান শূন্য হয়, তখন নির্ভরশীল চলক (Y) এর আনুমানিক মান কত হবে, সেটাই a। যেমন, যদি আপনি একদমই পড়াশোনা না করেন (X=0), তাহলে আপনার পরীক্ষার নম্বর কত হতে পারে, তার একটা আনুমানিক ধারণা।
b হলো স্লপ (Slope): এটি রেখার ঢাল বা খাড়া হওয়ার পরিমাণ নির্দেশ করে। এটি দেখায়, স্বাধীন চলক (X) এর মান যখন এক ইউনিট বাড়ে, তখন নির্ভরশীল চলক (Y) এর মান কতটুকু পরিবর্তন হয়। যেমন, যদি b এর মান ২ হয়, তার মানে পড়াশোনার সময় এক ঘণ্টা বাড়ালে পরীক্ষার নম্বর আনুমানিক ২ বাড়বে।
কেন আমরা লিনিয়ার রিগ্রেশন ব্যবহার করি? (Why Use It?)
এর প্রধান কাজ দুটো, যা গবেষণায় দারুণ কাজে আসে:
A) সম্পর্ক বোঝা (Understanding Relationships): এটি আপনাকে বলে দেবে, আপনার চলকগুলোর মধ্যে আদৌ কোনো সম্পর্ক আছে কি না, এবং সেই সম্পর্কটা কতটা শক্তিশালী। ধরুন, আপনি জানতে চান, বিজ্ঞাপনে খরচ বাড়ালে পণ্যের বিক্রি কি সত্যিই বাড়ে? যদি বাড়ে, তাহলে কতটা বাড়ে? লিনিয়ার রিগ্রেশন আপনাকে এই 'কতটা'র একটা সংখ্যাগত পরিমাপ দেবে।
B) ভবিষ্যৎ অনুমান করা (Making Predictions): একবার সম্পর্কটা বুঝে গেলে, আমরা ভবিষ্যৎ সম্পর্কে কিছু অনুমান করতে পারি। ধরুন, আপনি দেখলেন যে, তাপমাত্রা বাড়লে আইসক্রিমের বিক্রি বাড়ে। লিনিয়ার রিগ্রেশন আপনাকে একটি মডেল দেবে, যার মাধ্যমে আপনি হয়তো বলতে পারবেন, আগামী সপ্তাহে তাপমাত্রা যদি আরও বাড়ে, তাহলে আইসক্রিমের বিক্রি কেমন হতে পারে। এটি অনেকটা আবহাওয়ার পূর্বাভাস দেওয়ার মতো, যেখানে আমরা অতীতের ডেটা ব্যবহার করে ভবিষ্যতের একটা ধারণা পাই।
লিনিয়ার রিগ্রেশন কীভাবে কাজ করে? (How Does It Work?)
লিনিয়ার রিগ্রেশন কাজ করে একটা সরলরেখা ব্যবহার করে। ভাবুন, আপনার কাছে কিছু ডেটা পয়েন্ট আছে, যেমন গ্রাফ পেপারে ছড়ানো কিছু বিন্দু। লিনিয়ার রিগ্রেশনের কাজ হলো এই বিন্দুগুলোর মাঝখান দিয়ে এমন একটা সরলরেখা আঁকা, যা সব বিন্দু থেকে 'গড়ে' সবচেয়ে কম দূরত্বে থাকে। এই 'সবচেয়ে কম দূরত্ব' খুঁজে বের করার জন্য কিছু গাণিতিক হিসাব-নিকাশ করা হয়, যাকে আমরা 'এরর মিনিমাইজেশন' বা 'অবশিষ্ট কমানো' বলি। অর্থাৎ, ডেটা পয়েন্টগুলো থেকে রেখার যে দূরত্ব, সেই দূরত্বগুলোকে যতটা সম্ভব ছোট করা হয়, যাতে রেখাটি ডেটার 'প্রবণতা' বা 'ট্রেন্ড'কে সবচেয়ে ভালোভাবে দেখাতে পারে। এই রেখাটিই হলো আপনার রিগ্রেশন লাইন, যা আপনার ডেটার গল্পটা বলে।
লিনিয়ার রিগ্রেশনের প্রকারভেদ (Types of Linear Regression)
লিনিয়ার রিগ্রেশন মূলত দুটি প্রধান ধরনে বিভক্ত, নির্ভর করে আপনি কতগুলো স্বাধীন চলক ব্যবহার করছেন তার উপর:
সাধারণ লিনিয়ার রিগ্রেশন (Simple Linear Regression): এখানে শুধু একটি স্বাধীন চলক এবং একটি নির্ভরশীল চলক থাকে।
উদাহরণ: একজন ছাত্রের পড়াশোনার সময়ের (স্বাধীন চলক) সাথে তার পরীক্ষার নম্বরের (নির্ভরশীল চলক) সম্পর্ক। এখানে আপনি শুধু একটি কারণ (পড়াশোনার সময়) দিয়ে একটি ফলাফল (পরীক্ষার নম্বর) বোঝার চেষ্টা করছেন।
মাল্টিপল লিনিয়ার রিগ্রেশন (Multiple Linear Regression): এখানে একাধিক স্বাধীন চলক এবং একটি নির্ভরশীল চলক থাকে।
উদাহরণ: একটি বাড়ির দাম (নির্ভরশীল চলক) শুধু তার আকারের উপর নির্ভর করে না, বরং এলাকার অবস্থান, বাড়ির বয়স, রুমের সংখ্যা, বাথরুমের সংখ্যা – এই সবকিছুর উপর নির্ভর করে। মাল্টিপল রিগ্রেশন এই সব কারণ একসঙ্গে বিশ্লেষণ করে দেখায় যে, কোন কারণটি বাড়ির দামের উপর কতটা প্রভাব ফেলছে। এটি অনেকটা অনেকগুলো কারণ একসঙ্গে একটি ফলাফলের উপর কীভাবে প্রভাব ফেলে, তা দেখার মতো।
কিছু জরুরি কথা (Key Concepts): অবশিষ্ট (Residuals): রিগ্রেশন রেখাটি সব ডেটা পয়েন্টের উপর দিয়ে যায় না, কিছু পয়েন্ট রেখার উপরে বা নিচে থাকে। এই ডেটা পয়েন্ট এবং রেখার মধ্যে যে দূরত্ব, সেটিই হলো অবশিষ্ট বা এরর (error)। এটি দেখায়, আমাদের মডেল কতটা নিখুঁতভাবে অনুমান করতে পারছে। যত কম অবশিষ্ট, মডেল তত ভালো।
সহসম্পর্ক (Correlation): এটি লিনিয়ার রিগ্রেশনের সাথে জড়িত একটি ধারণা। সহসম্পর্ক (যেমন পিয়ারসন কোরিলেশন কোএফিশিয়েন্ট) দুটি চলকের মধ্যে সম্পর্কের শক্তি এবং দিক (ইতিবাচক বা নেতিবাচক) পরিমাপ করে। লিনিয়ার রিগ্রেশন এই সম্পর্ককে একটি মডেলের মাধ্যমে ব্যাখ্যা করে। সহসম্পর্ক আপনাকে বলবে সম্পর্ক আছে কিনা, আর রিগ্রেশন আপনাকে বলবে সেই সম্পর্কটা কেমন এবং কীভাবে কাজ করে।
অনুমান (Assumptions): লিনিয়ার রিগ্রেশন কিছু নির্দিষ্ট শর্তের উপর ভিত্তি করে কাজ করে। যেমন, চলকগুলোর মধ্যে সম্পর্কটা যেন সত্যিই সরলরৈখিক হয়, ডেটা পয়েন্টগুলো যেন খুব বেশি ছড়ানো-ছিটানো না থাকে (আউটলায়ার না থাকে), এবং এররগুলো যেন এলোমেলোভাবে ছড়ানো থাকে। এই শর্তগুলো পূরণ হলে মডেলের ফলাফল আরও নির্ভরযোগ্য হয়।
কখন ব্যবহার করবেন, কখন করবেন না? (When to Use, When Not to Use?)
কখন ব্যবহার করবেন?: যখন আপনি দুটি বা তার বেশি চলকের মধ্যে একটি সরলরৈখিক সম্পর্ক আছে বলে মনে করেন এবং সেই সম্পর্কটা বুঝতে চান। যখন আপনি একটি চলকের মান ব্যবহার করে অন্য একটি চলকের মান অনুমান করতে চান।
যখন আপনি জানতে চান, কোন কারণগুলো (স্বাধীন চলক) একটি নির্দিষ্ট ফলাফলের (নির্ভরশীল চলক) উপর সবচেয়ে বেশি প্রভাব ফেলছে। যখন আপনি কোনো ধারাবাহিক ফলাফল (continuous outcome) যেমন, তাপমাত্রা, বিক্রি, নম্বর ইত্যাদি অনুমান করতে চান।
কখন করবেন না?
যদি চলকগুলোর মধ্যে কোনো সরলরৈখিক সম্পর্ক না থাকে (যেমন, সম্পর্কটি বক্ররেখার মতো বা এলোমেলো)। এক্ষেত্রে অন্য ধরনের রিগ্রেশন মডেল ব্যবহার করতে হতে পারে। যদি আপনার ডেটায় অনেক বেশি অস্বাভাবিক বা ভুল ডেটা (outliers) থাকে, যা রেখাটিকে ভুলভাবে প্রভাবিত করতে পারে। এই 'আউটলায়ার'গুলো ফলাফলকে ভুল পথে চালিত করতে পারে।
যদি আপনার স্বাধীন চলকগুলো একে অপরের সাথে খুব বেশি সম্পর্কিত হয় (multicollinearity), তাহলে মাল্টিপল রিগ্রেশন ব্যবহার করা কঠিন হতে পারে। এটি অনেকটা এমন যে, দুটি কারণ একই রকম প্রভাব ফেলছে, তখন বোঝা কঠিন হয়ে যায় কোনটি আসল প্রভাবক।
লিনিয়ার রিগ্রেশন হলো ডেটা বিশ্লেষণের এক দারুণ হাতিয়ার, যা আপনাকে ডেটার ভেতরের লুকানো গল্পগুলো খুঁজে বের করতে সাহায্য করবে। এটি শুধু সংখ্যা নয়, বরং সংখ্যার পেছনের কারণ ও প্রভাবকে বুঝতে শেখায়। আশা করি, এই বিস্তারিত আলোচনা আপনার লিনিয়ার রিগ্রেশন সম্পর্কে ধারণা আরও পরিষ্কার করেছে। আপনার যদি আরও কিছু জানার থাকে, তাহলে আমাকে জানাতে পারেন!
Md. Rony Masud
BBA, MBA (DU), MS (Japan)
আপনার গবেষণা পদ্ধতির সাতকাহন: লিনিয়ার রিগ্রেশন
(Linear Regression in Research methodology)
ধরুন, আপনি অনেকগুলো কাঁচামাল জোগাড় করেছেন। এখন সেই কাঁচামাল দিয়ে কী বানাবেন, কীভাবে বানাবেন, সেটাই হলো বিশ্লেষণের কাজ। আর এই বিশ্লেষণের দুনিয়ায় একটা দারুণ 'ম্যাজিক টুল' আছে, যার নাম লিনিয়ার রিগ্রেশন। এর নামটা একটু জটিল শোনালেও, এর কাজটা কিন্তু খুবই সহজ আর কাজের। চলুন, আজ আমরা এই লিনিয়ার রিগ্রেশনের আদ্যোপান্ত জেনে নিই, একদম A2Z!
লিনিয়ার রিগ্রেশন আসলে কী? (What is Linear Regression?)
আচ্ছা, আপনি কি কখনো ভেবে দেখেছেন, একজন শিক্ষার্থী যত বেশি সময় পড়াশোনা করে, তার পরীক্ষার নম্বর তত বাড়ে কেন? অথবা, একটি পণ্যের দাম বাড়লে তার বিক্রি কমে যায় কেন? এই 'কেন' আর 'কীভাবে'র সম্পর্কটা খুঁজে বের করার জন্যই লিনিয়ার রিগ্রেশনকে আমরা ব্যবহার করি।
সহজ করে বললে, লিনিয়ার রিগ্রেশন হলো এমন একটি পরিসংখ্যানগত কৌশল, যা দুটি বা তার বেশি বিষয়ের মধ্যে একটা সরলরেখার মতো সম্পর্ক খুঁজে বের করতে সাহায্য করে। এটি অনেকটা একটা অদৃশ্য সুতো খুঁজে বের করার মতো, যা দুটি জিনিসকে একসঙ্গে বেঁধে রাখে। যেমন, পড়াশোনার সময় আর পরীক্ষার নম্বরের মধ্যে একটা সম্পর্ক আছে, তাই না? লিনিয়ার রিগ্রেশন সেই সম্পর্কটাকে একটা সরলরেখা দিয়ে প্রকাশ করে।
এখানে দুটো গুরুত্বপূর্ণ খেলোয়াড় আছে, যাদেরকে আমরা 'চলক' (Variables) বলি:
১। স্বাধীন চলক (Independent Variable): এই হলো সেই 'কারণ' বা 'ইনপুট'। একে আপনি পরিবর্তন করতে পারেন, বা এটি নিজে নিজেই পরিবর্তিত হয় এবং অন্য কোনো কিছুকে প্রভাবিত করে। যেমন, পড়াশোনার সময়, বিজ্ঞাপনের খরচ, বা একটি বাড়ির আকার। ভাবুন তো, পড়াশোনার সময় বাড়লে বা কমলে পরীক্ষার নম্বরের ওপর একটা প্রভাব পড়ে, তাই না?
২। নির্ভরশীল চলক (Dependent Variable): আর এই হলো সেই 'ফলাফল' বা 'আউটপুট', যা স্বাধীন চলকের পরিবর্তনের কারণে প্রভাবিত হয়। যেমন, পরীক্ষার নম্বর, পণ্যের বিক্রি, বা বাড়ির দাম। এই চলকটি স্বাধীন চলকের উপর 'নির্ভর' করে।
লিনিয়ার রিগ্রেশনের মূল লক্ষ্য হলো এই স্বাধীন ও নির্ভরশীল চলকের মধ্যে একটা গাণিতিক সম্পর্ক খুঁজে বের করা, যা দেখতে একটা সরলরেখার মতো। এই রেখার একটা সমীকরণ থাকে: Y=a+bX
এখানে: Y হলো নির্ভরশীল চলক (ফলাফল): অর্থাৎ, আপনি যে জিনিসটা অনুমান করতে চান বা যার পরিবর্তন মাপতে চান।
X হলো স্বাধীন চলক (কারণ): অর্থাৎ, যে জিনিসটা পরিবর্তনের কারণ হিসেবে কাজ করছে।
a হলো ইন্টারসেপ্ট (Intercept): এটি অনেকটা গ্রাফের Y-অক্ষকে রেখাটি যেখানে ছেদ করে সেই বিন্দু। সহজ ভাষায়, যখন স্বাধীন চলক (X) এর মান শূন্য হয়, তখন নির্ভরশীল চলক (Y) এর আনুমানিক মান কত হবে, সেটাই a। যেমন, যদি আপনি একদমই পড়াশোনা না করেন (X=0), তাহলে আপনার পরীক্ষার নম্বর কত হতে পারে, তার একটা আনুমানিক ধারণা।
b হলো স্লপ (Slope): এটি রেখার ঢাল বা খাড়া হওয়ার পরিমাণ নির্দেশ করে। এটি দেখায়, স্বাধীন চলক (X) এর মান যখন এক ইউনিট বাড়ে, তখন নির্ভরশীল চলক (Y) এর মান কতটুকু পরিবর্তন হয়। যেমন, যদি b এর মান ২ হয়, তার মানে পড়াশোনার সময় এক ঘণ্টা বাড়ালে পরীক্ষার নম্বর আনুমানিক ২ বাড়বে।
কেন আমরা লিনিয়ার রিগ্রেশন ব্যবহার করি? (Why Use It?)
এর প্রধান কাজ দুটো, যা গবেষণায় দারুণ কাজে আসে:
A) সম্পর্ক বোঝা (Understanding Relationships): এটি আপনাকে বলে দেবে, আপনার চলকগুলোর মধ্যে আদৌ কোনো সম্পর্ক আছে কি না, এবং সেই সম্পর্কটা কতটা শক্তিশালী। ধরুন, আপনি জানতে চান, বিজ্ঞাপনে খরচ বাড়ালে পণ্যের বিক্রি কি সত্যিই বাড়ে? যদি বাড়ে, তাহলে কতটা বাড়ে? লিনিয়ার রিগ্রেশন আপনাকে এই 'কতটা'র একটা সংখ্যাগত পরিমাপ দেবে।
B) ভবিষ্যৎ অনুমান করা (Making Predictions): একবার সম্পর্কটা বুঝে গেলে, আমরা ভবিষ্যৎ সম্পর্কে কিছু অনুমান করতে পারি। ধরুন, আপনি দেখলেন যে, তাপমাত্রা বাড়লে আইসক্রিমের বিক্রি বাড়ে। লিনিয়ার রিগ্রেশন আপনাকে একটি মডেল দেবে, যার মাধ্যমে আপনি হয়তো বলতে পারবেন, আগামী সপ্তাহে তাপমাত্রা যদি আরও বাড়ে, তাহলে আইসক্রিমের বিক্রি কেমন হতে পারে। এটি অনেকটা আবহাওয়ার পূর্বাভাস দেওয়ার মতো, যেখানে আমরা অতীতের ডেটা ব্যবহার করে ভবিষ্যতের একটা ধারণা পাই।
লিনিয়ার রিগ্রেশন কীভাবে কাজ করে? (How Does It Work?)
লিনিয়ার রিগ্রেশন কাজ করে একটা সরলরেখা ব্যবহার করে। ভাবুন, আপনার কাছে কিছু ডেটা পয়েন্ট আছে, যেমন গ্রাফ পেপারে ছড়ানো কিছু বিন্দু। লিনিয়ার রিগ্রেশনের কাজ হলো এই বিন্দুগুলোর মাঝখান দিয়ে এমন একটা সরলরেখা আঁকা, যা সব বিন্দু থেকে 'গড়ে' সবচেয়ে কম দূরত্বে থাকে। এই 'সবচেয়ে কম দূরত্ব' খুঁজে বের করার জন্য কিছু গাণিতিক হিসাব-নিকাশ করা হয়, যাকে আমরা 'এরর মিনিমাইজেশন' বা 'অবশিষ্ট কমানো' বলি। অর্থাৎ, ডেটা পয়েন্টগুলো থেকে রেখার যে দূরত্ব, সেই দূরত্বগুলোকে যতটা সম্ভব ছোট করা হয়, যাতে রেখাটি ডেটার 'প্রবণতা' বা 'ট্রেন্ড'কে সবচেয়ে ভালোভাবে দেখাতে পারে। এই রেখাটিই হলো আপনার রিগ্রেশন লাইন, যা আপনার ডেটার গল্পটা বলে।
লিনিয়ার রিগ্রেশনের প্রকারভেদ (Types of Linear Regression)
লিনিয়ার রিগ্রেশন মূলত দুটি প্রধান ধরনে বিভক্ত, নির্ভর করে আপনি কতগুলো স্বাধীন চলক ব্যবহার করছেন তার উপর:
সাধারণ লিনিয়ার রিগ্রেশন (Simple Linear Regression): এখানে শুধু একটি স্বাধীন চলক এবং একটি নির্ভরশীল চলক থাকে।
উদাহরণ: একজন ছাত্রের পড়াশোনার সময়ের (স্বাধীন চলক) সাথে তার পরীক্ষার নম্বরের (নির্ভরশীল চলক) সম্পর্ক। এখানে আপনি শুধু একটি কারণ (পড়াশোনার সময়) দিয়ে একটি ফলাফল (পরীক্ষার নম্বর) বোঝার চেষ্টা করছেন।
মাল্টিপল লিনিয়ার রিগ্রেশন (Multiple Linear Regression): এখানে একাধিক স্বাধীন চলক এবং একটি নির্ভরশীল চলক থাকে।
উদাহরণ: একটি বাড়ির দাম (নির্ভরশীল চলক) শুধু তার আকারের উপর নির্ভর করে না, বরং এলাকার অবস্থান, বাড়ির বয়স, রুমের সংখ্যা, বাথরুমের সংখ্যা – এই সবকিছুর উপর নির্ভর করে। মাল্টিপল রিগ্রেশন এই সব কারণ একসঙ্গে বিশ্লেষণ করে দেখায় যে, কোন কারণটি বাড়ির দামের উপর কতটা প্রভাব ফেলছে। এটি অনেকটা অনেকগুলো কারণ একসঙ্গে একটি ফলাফলের উপর কীভাবে প্রভাব ফেলে, তা দেখার মতো।
কিছু জরুরি কথা (Key Concepts): অবশিষ্ট (Residuals): রিগ্রেশন রেখাটি সব ডেটা পয়েন্টের উপর দিয়ে যায় না, কিছু পয়েন্ট রেখার উপরে বা নিচে থাকে। এই ডেটা পয়েন্ট এবং রেখার মধ্যে যে দূরত্ব, সেটিই হলো অবশিষ্ট বা এরর (error)। এটি দেখায়, আমাদের মডেল কতটা নিখুঁতভাবে অনুমান করতে পারছে। যত কম অবশিষ্ট, মডেল তত ভালো।
সহসম্পর্ক (Correlation): এটি লিনিয়ার রিগ্রেশনের সাথে জড়িত একটি ধারণা। সহসম্পর্ক (যেমন পিয়ারসন কোরিলেশন কোএফিশিয়েন্ট) দুটি চলকের মধ্যে সম্পর্কের শক্তি এবং দিক (ইতিবাচক বা নেতিবাচক) পরিমাপ করে। লিনিয়ার রিগ্রেশন এই সম্পর্ককে একটি মডেলের মাধ্যমে ব্যাখ্যা করে। সহসম্পর্ক আপনাকে বলবে সম্পর্ক আছে কিনা, আর রিগ্রেশন আপনাকে বলবে সেই সম্পর্কটা কেমন এবং কীভাবে কাজ করে।
অনুমান (Assumptions): লিনিয়ার রিগ্রেশন কিছু নির্দিষ্ট শর্তের উপর ভিত্তি করে কাজ করে। যেমন, চলকগুলোর মধ্যে সম্পর্কটা যেন সত্যিই সরলরৈখিক হয়, ডেটা পয়েন্টগুলো যেন খুব বেশি ছড়ানো-ছিটানো না থাকে (আউটলায়ার না থাকে), এবং এররগুলো যেন এলোমেলোভাবে ছড়ানো থাকে। এই শর্তগুলো পূরণ হলে মডেলের ফলাফল আরও নির্ভরযোগ্য হয়।
কখন ব্যবহার করবেন, কখন করবেন না? (When to Use, When Not to Use?)
কখন ব্যবহার করবেন?: যখন আপনি দুটি বা তার বেশি চলকের মধ্যে একটি সরলরৈখিক সম্পর্ক আছে বলে মনে করেন এবং সেই সম্পর্কটা বুঝতে চান। যখন আপনি একটি চলকের মান ব্যবহার করে অন্য একটি চলকের মান অনুমান করতে চান।
যখন আপনি জানতে চান, কোন কারণগুলো (স্বাধীন চলক) একটি নির্দিষ্ট ফলাফলের (নির্ভরশীল চলক) উপর সবচেয়ে বেশি প্রভাব ফেলছে। যখন আপনি কোনো ধারাবাহিক ফলাফল (continuous outcome) যেমন, তাপমাত্রা, বিক্রি, নম্বর ইত্যাদি অনুমান করতে চান।
কখন করবেন না?
যদি চলকগুলোর মধ্যে কোনো সরলরৈখিক সম্পর্ক না থাকে (যেমন, সম্পর্কটি বক্ররেখার মতো বা এলোমেলো)। এক্ষেত্রে অন্য ধরনের রিগ্রেশন মডেল ব্যবহার করতে হতে পারে। যদি আপনার ডেটায় অনেক বেশি অস্বাভাবিক বা ভুল ডেটা (outliers) থাকে, যা রেখাটিকে ভুলভাবে প্রভাবিত করতে পারে। এই 'আউটলায়ার'গুলো ফলাফলকে ভুল পথে চালিত করতে পারে।
যদি আপনার স্বাধীন চলকগুলো একে অপরের সাথে খুব বেশি সম্পর্কিত হয় (multicollinearity), তাহলে মাল্টিপল রিগ্রেশন ব্যবহার করা কঠিন হতে পারে। এটি অনেকটা এমন যে, দুটি কারণ একই রকম প্রভাব ফেলছে, তখন বোঝা কঠিন হয়ে যায় কোনটি আসল প্রভাবক।
লিনিয়ার রিগ্রেশন হলো ডেটা বিশ্লেষণের এক দারুণ হাতিয়ার, যা আপনাকে ডেটার ভেতরের লুকানো গল্পগুলো খুঁজে বের করতে সাহায্য করবে। এটি শুধু সংখ্যা নয়, বরং সংখ্যার পেছনের কারণ ও প্রভাবকে বুঝতে শেখায়। আশা করি, এই বিস্তারিত আলোচনা আপনার লিনিয়ার রিগ্রেশন সম্পর্কে ধারণা আরও পরিষ্কার করেছে। আপনার যদি আরও কিছু জানার থাকে, তাহলে আমাকে জানাতে পারেন!
Md. Rony Masud
BBA, MBA (DU), MS (Japan)